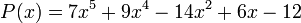polinomios: Ejemplos

Por ejemplo:

$x^{2} - 4x + 7 \;$

es un polinomio, pero:

$x^{2} - \frac{4}{x} +7 x^{\frac{3}{2}}$

no, porque incorpora la división y un exponente fraccionario.

El polinomio de un sólo término se denomina monomio, el de dos, binomio, el de tres, trinomio, el de cuatro cuadrinomio, o polinomio de "N" términos dependiendo de cuantos haya.

La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:

$P(x)= a_n x^{n} + a_{n-1} x^{n-1} + a_{n-2} x^{n-2} + \cdots + a_2 x^2 + a_1 x + a_0 \,$

por ejemplo:

$P(x)= 7 x^5 + 9 x^4 - 14 x^2 + 6 x - 12 \,$

Se denomina grado de un polinomio a la mayor potencia de los monomios que lo componen.

Multiplicación de polinomios

La multiplicación de polinomios es una operación matemática que tiene por objeto obtener un producto a partir de dos expresiones algebraicas denominadas factores.
Al igual que para la suma en la multiplicación el orden de los factores no altera el producto, denominándose esta característica propiedad conmutativa.
Ejeplo:

Los factores de una multiplicación pueden agruparse de cualquier modo demostrando con esto que la multiplicación cumple la ley asociativa.
Ejemplo:

Leyes de la multiplicación
Para la multiplicación se hace necesario tener en cuenta la ley de los signos, la cual postula que signos iguales dan un producto positivo y signos diferentes dan un producto negativo.
Ejemplo:

Cuando se multiplican expresiones con la misma denominación es decir la misma letra, el producto se obtiene dejando la misma letra y sumando sus exponentes.
Ejemplo:

El producto de dos términos es el producto de sus coeficientes es decir los números que acompañan a las letras.
Ejemplo:

Como en el caso de la adición que la resta no se tiene en cuenta por que el signo del monomio determina si el resultado aumenta o disminuye, en el caso de la multiplicación sucede algo análogo dado que al multiplicar por el inverso se obtiene el mismo resultado que multiplicando.
El inverso de un polinomio en este caso es la unidad dividida por el mismo polinomio, el cociente de esta división se le denomina inverso del polinomio.
Ejemplo:

En las expresiones algebraicas en las cuales hay fracciones el producto se obtiene multiplicando solamente el numerado por otro factor, si el otro factor también es fraccionario el producto se obtiene multiplicando los numeradores y los denominadores entre si.
Ejemplo: